Cocolib

Appearance

On this page

完全二叉树的节点个数 ​

Question

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

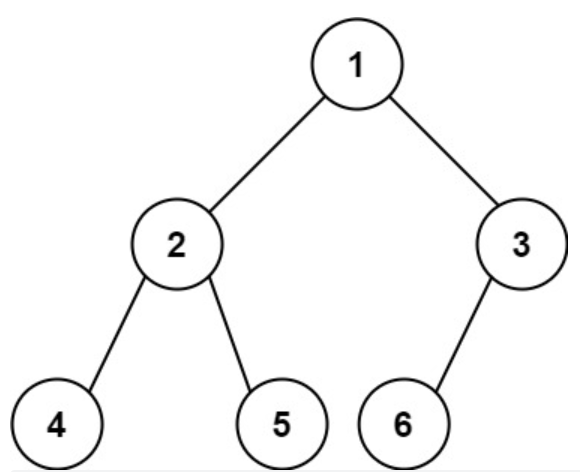
image-20230612103741887

求普通二叉树的节点个数 ​

  • 可以用前中后序遍历来做

  • 可以用层序遍历来做

前序遍历 ​

js
var countNodes = function(root) {
    let arr = []
    digui(root,arr)
    return arr.length
};

var digui = function(root,arr){
    if(root===null) return
    arr.push(root.val)			//前
    digui(root.left,arr)
    digui(root.right,arr)
}

层序遍历 ​

js
var countNodes = function(root) {
    return levelOrder(root)
};

var levelOrder = function(root) {
    const queue = []
    const ans = []
    if(root!=null)  
        queue.push(root)
    let index = 0                   //记录第几层
    let count = 0                   //记录节点个数
    while(queue.length!=0){
        ans.push([])
        let len = queue.length      //记录该层有几个节点
        for(let i=0;i<len;i++){
            let p = queue.shift()   //shift() 方法从数组中删除第一个元素，并返回该元素的值
            ans[index].push(p.val)
            count++
            if(p.left!=null)   queue.push(p.left)
            if(p.right!=null)   queue.push(p.right)
        }
        index++
    }
    return count
};

利用完全二叉树特性 ​

img

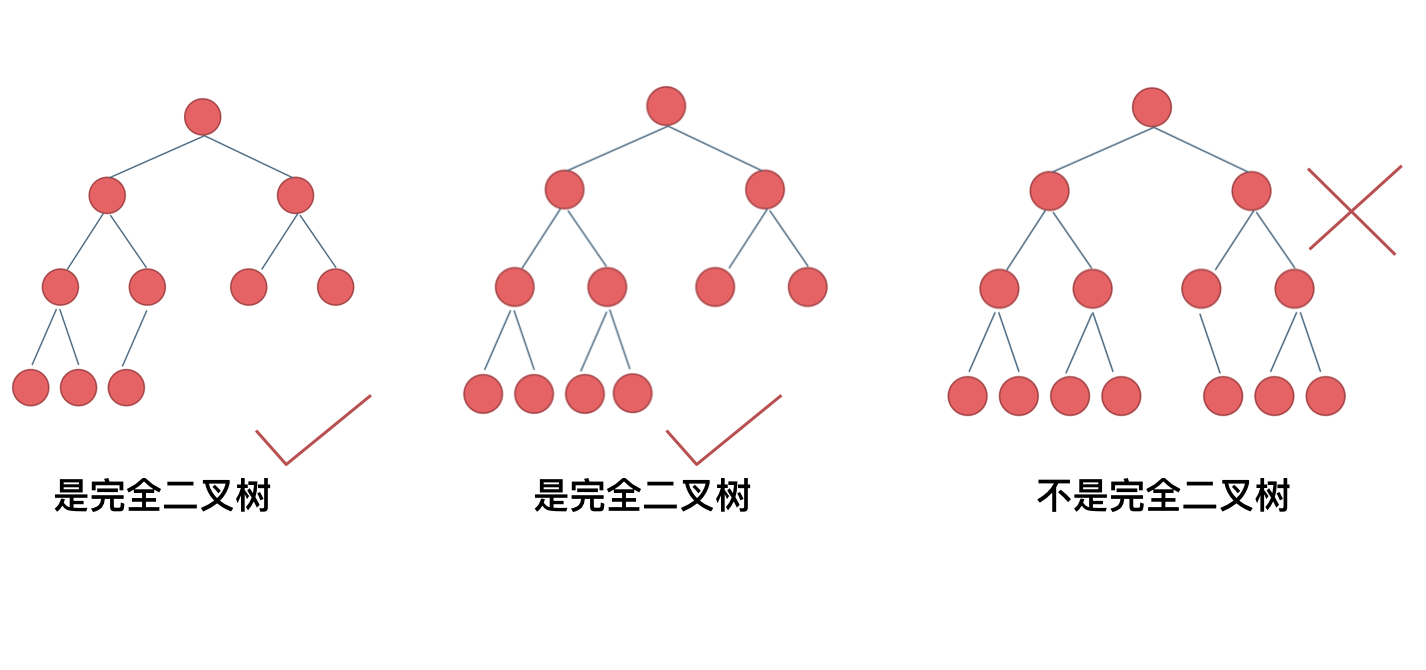
完全二叉树只有两种情况，情况一：就是满二叉树，情况二：最后一层叶子节点没有满。

  • 对于情况一，可以直接用 2^h 来计算。

  • 对于情况二，分别递归左孩子，和右孩子，递归到某一深度一定会有左孩子或者右孩子为满二叉树，然后依然可以按照情况1来计算。

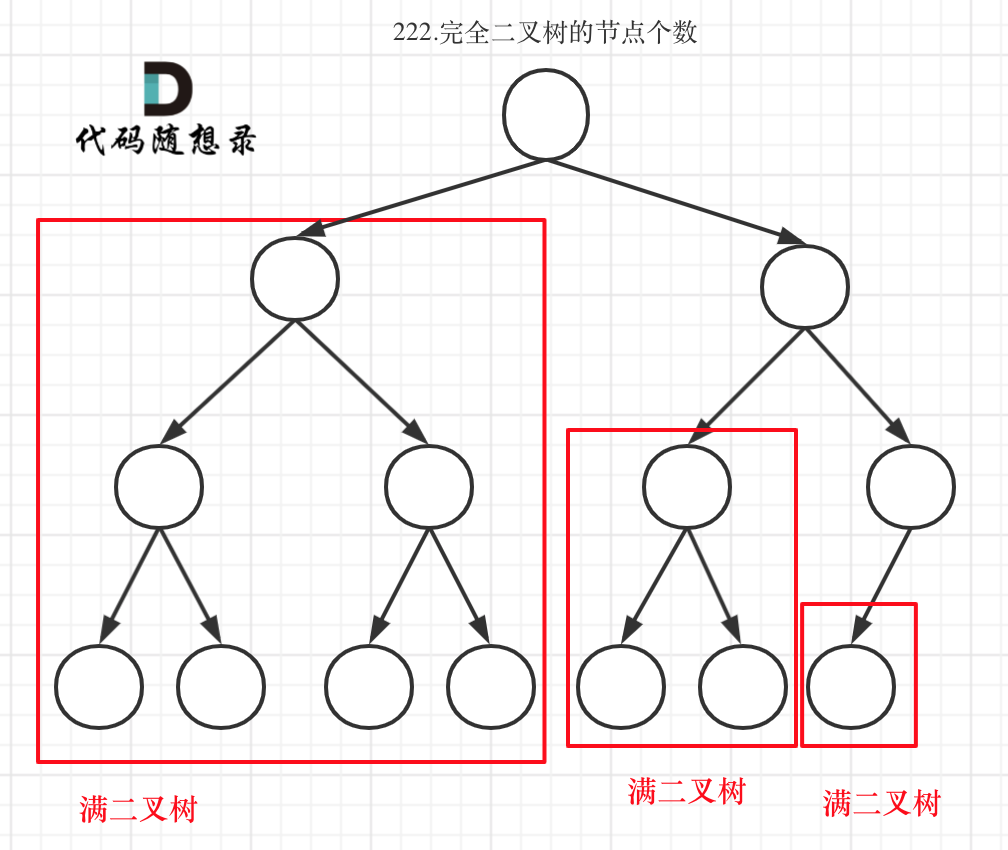
222.完全二叉树的节点个数

可以看出如果整个树不是满二叉树，就递归其左右孩子，直到遇到满二叉树为止，用公式计算这个子树（满二叉树）的节点数量。

这里关键在于如何去判断一个左子树或者右子树是不是满二叉树呢？

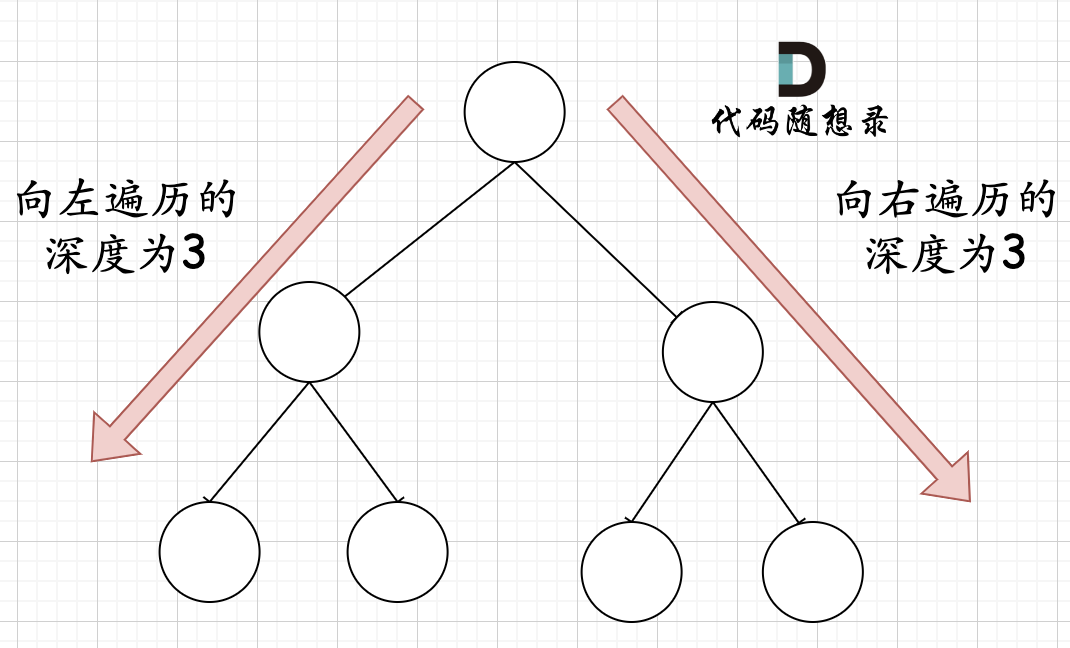
在完全二叉树中，如果递归向左遍历的深度等于递归向右遍历的深度，那说明就是满二叉树。如图：

img

在完全二叉树中，如果递归向左遍历的深度不等于递归向右遍历的深度，则说明不是满二叉树，如图：

img

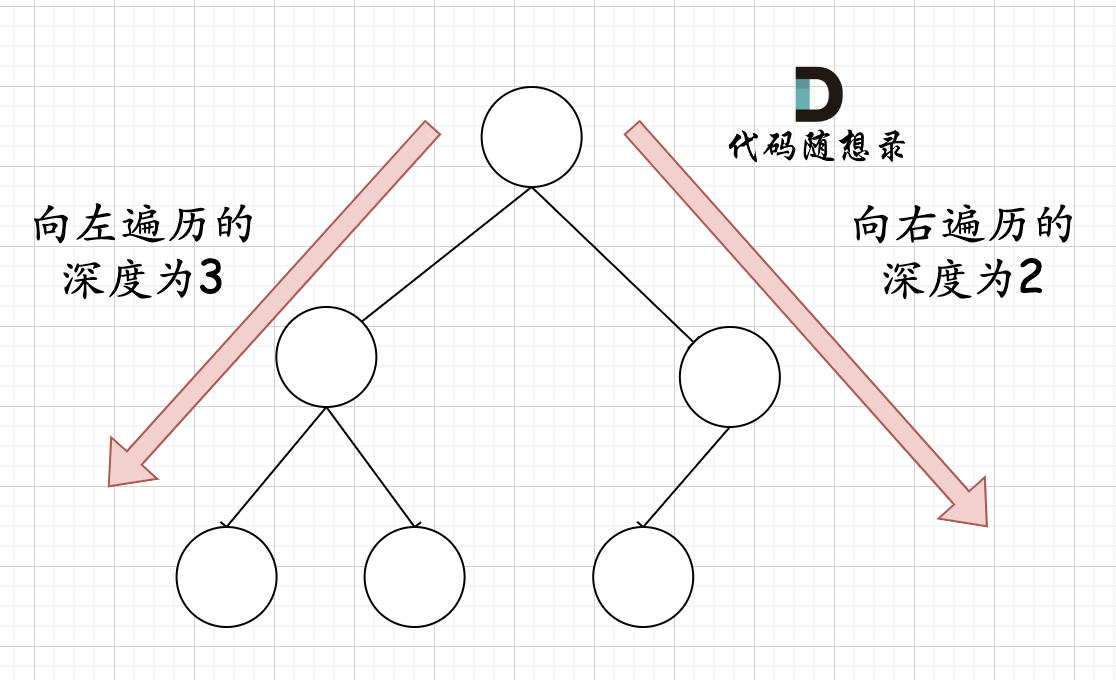
那有录友说了，这种情况，递归向左遍历的深度等于递归向右遍历的深度，但也不是满二叉树，如题：

img

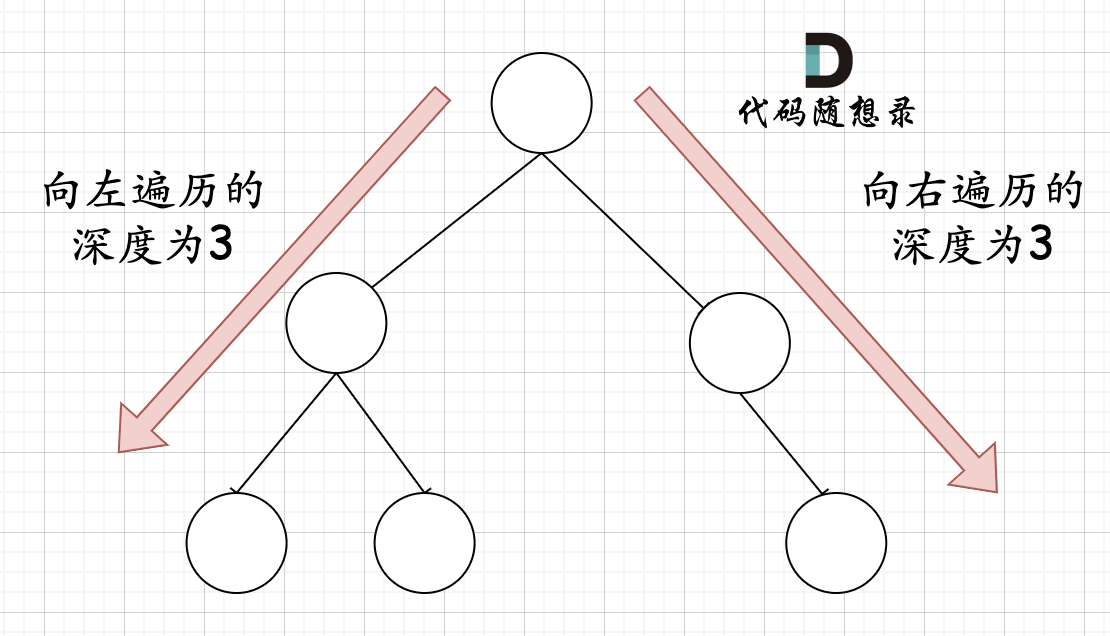
如果这么想，大家就是对 完全二叉树理解有误区了，以上这棵二叉树，它根本就不是一个完全二叉树！

js
var countNodes = function(root) {
    let leftNum = 0,rightNum = 0;
    if(root==null)  return 0;
    let pLeft = root.left;
    let pRight = root.right;
    while(pLeft!=null){                                 //1、分别遍历左右两侧
        leftNum++;
        pLeft = pLeft.left;
    }
    while(pRight!=null){
        rightNum++;
        pRight = pRight.right;
    }
    if(leftNum==rightNum)   return (2<<leftNum)-1;    	//2、如果为满二叉树
    leftNum = countNodes(root.left);                     //3、单层逻辑
    rightNum = countNodes(root.right);
    return leftNum+rightNum+1;
};