理论基础
动归难就难在怎么找**dp[i]和dp[i-1]的关系**
1、0-1背包
二维dp数组01背包
js
// 定义 dp 数组
const len = weight.length,
let dp = Array(len+1).fill().map(() => Array(size + 1).fill(0));
// 初始化
for(let j = weight[0]; j <= size; j++) {
dp[0][j] = value[0];
}
// weight 数组的长度len 就是物品个数
for(let i = 1; i <= len; i++) { // 遍历物品
for(let j = 0; j <= size; j++) { // 遍历背包容量
if(j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
console.table(dp)
return dp[len][size];一维dp数组(滚动数组)
js
const len = wight.length,
let dp = Array(size + 1).fill(0);
for(let i = 1; i <= len; i++) { // 遍历物品
for(let j = size; j >= wight[i - 1]; j--) { // 遍历背包
dp[j] = Math.max(dp[j], value[i - 1] + dp[j - wight[i - 1]]);
}
}
return dp[size];2、完全背包
完全背包和01背包问题唯一不同的地方就是,每种物品有无限件。
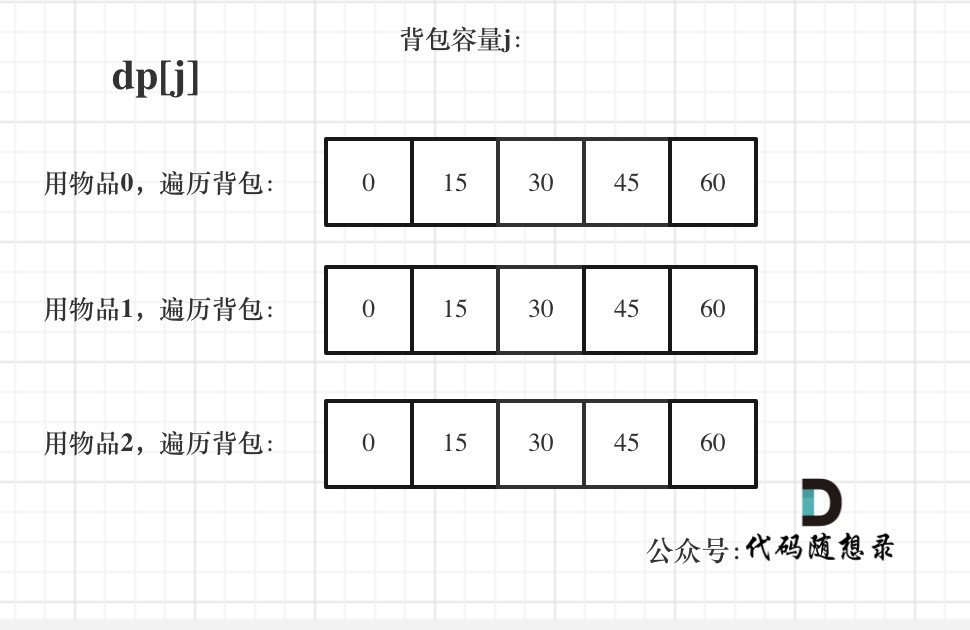
js
// 先遍历物品,再遍历背包
for(let i = 0; i < weight.size(); i++) { // 遍历物品
for(let j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}3、多重背包
有N种物品和一个容量为V 的背包。第i种物品最多有Mi件可用,每件耗费的空间是Ci ,价值是Wi 。求解将哪些物品装入背包可使这些物品的耗费的空间 总和不超过背包容量,且价值总和最大。
多重背包和01背包是非常像的, 为什么和01背包像呢?
每件物品最多有Mi件可用,把Mi件摊开,其实就是一个01背包问题了。
例如:背包最大重量为10。
物品为:
| 重量 | 价值 | 数量 | |
|---|---|---|---|
| 物品0 | 1 | 15 | 2 |
| 物品1 | 3 | 20 | 3 |
| 物品2 | 4 | 30 | 2 |
问背包能背的物品最大价值是多少?
和如下情况有区别么?
| 重量 | 价值 | 数量 | |
|---|---|---|---|
| 物品0 | 1 | 15 | 1 |
| 物品0 | 1 | 15 | 1 |
| 物品1 | 3 | 20 | 1 |
| 物品1 | 3 | 20 | 1 |
| 物品1 | 3 | 20 | 1 |
| 物品2 | 4 | 30 | 1 |
| 物品2 | 4 | 30 | 1 |
毫无区别,这就转成了一个01背包问题了,且每个物品只用一次。
背包问题总结
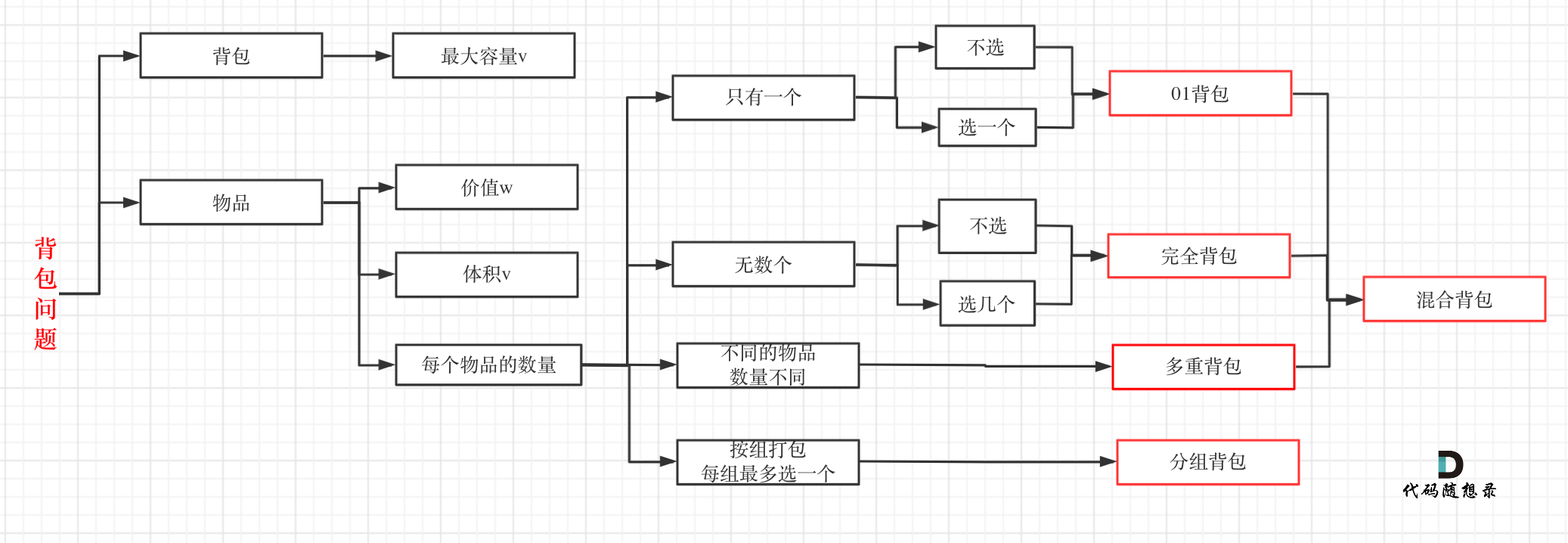
递推公式
问能否能装满背包(或者最多装多少):
dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);,对应题目如下:问装满背包有几种方法:
dp[j] += dp[j - nums[i]],对应题目如下:问背包装满最大价值:
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);,对应题目如下:问装满背包所有物品的最小个数:
dp[j] = min(dp[j - coins[i]] + 1, dp[j]);,对应题目如下:
遍历顺序
01背包
二维dp数组
先遍历物品还是先遍历背包都是可以的,且第二层for循环是从小到大遍历。
一维dp数组
只能先遍历物品再遍历背包容量,且第二层for循环是从大到小遍历。
完全背包
一维dp数组
先遍历物品还是先遍历背包都是可以的,且第二层for循环是从小到大遍历。
求组合数
外层for循环遍历物品,内层for遍历背包
求排列数
外层for遍历背包,内层for循环遍历物品
 Cocolib
Cocolib