组合总和II

Question

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次 。

注意：解集不能包含重复的组合。

思路

本题的难点在于区别2中：集合（数组candidates）有重复元素，但还不能有重复的组合。

都知道组合问题可以抽象为树形结构，那么“使用过”在这个树形结构上是有两个维度的，一个维度是同一树枝上使用过，一个维度是同一树层上使用过。没有理解这两个层面上的“使用过” 是造成大家没有彻底理解去重的根本原因。

那么问题来了，我们是要同一树层上使用过，还是同一树枝上使用过呢？

回看一下题目，元素在同一个组合内是可以重复的，怎么重复都没事，但两个组合不能相同。

所以我们要去重的是同一树层上的“使用过”，同一树枝上的都是一个组合里的元素，不用去重。

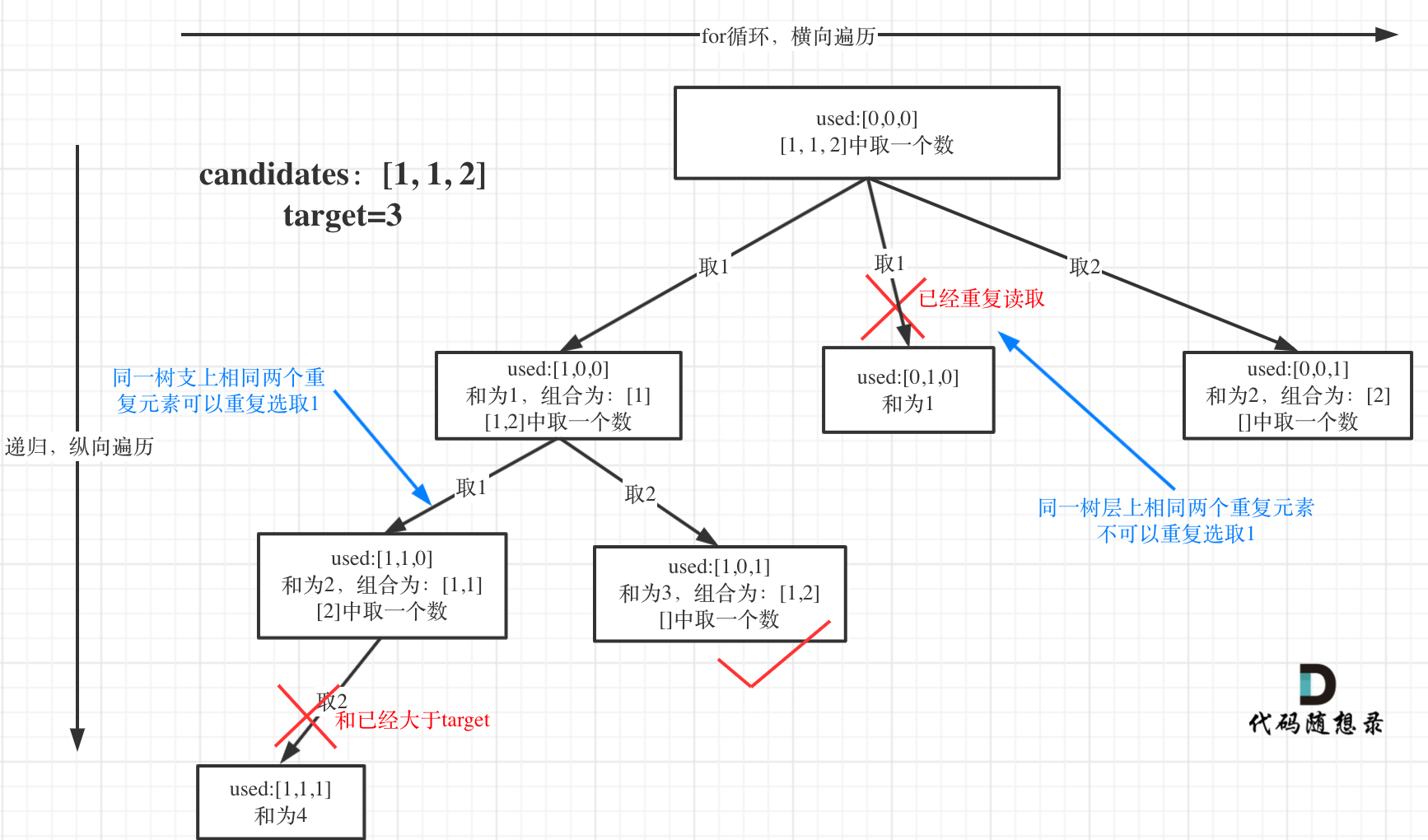
这种情况没有做到树层去重

var combinationSum2 = function(candidates, target) {
    const res = []  // 结果[][]
    const path = [] // 每次递归的结果[]
    let sum = target
    // startIndex ：每次递归的起使位置
    const backtracking = (startIndex)=>{
        if (sum < 0) { // 剪枝操作
            return; // 如果path.size() == k 但sum != n 直接返回
        }
        if( sum===0 ){		//终止条件
            res.push([...path])		
            return
        }
        for(let i=startIndex; i< candidates.length; i++){	// 本层集合中元素
            if(sum-candidates[i] < 0 ) continue //剪枝优化
            path.push(candidates[i])	
            sum-= candidates[i]			
            backtracking(i+1)		//树枝去重
            path.pop()
            sum+= candidates[i]			
        }
    }
    backtracking(0)
    return res
};

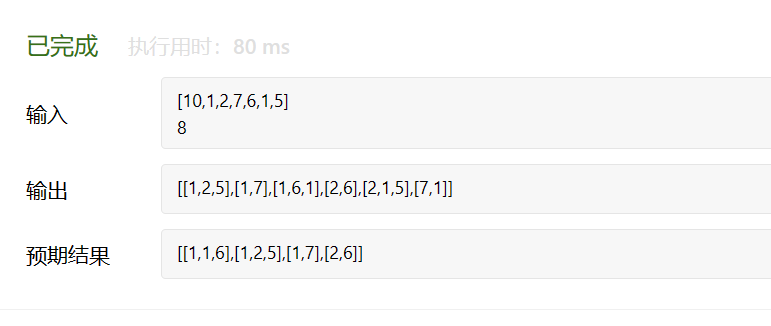
树层去重

进入递归之前首先对数组进行排序，使数值相同的元素相邻
使用used[]记录已经使用过的元素
关键应该理解：if(i>0&&candidates[i]===candidates[i-1]&&used[i-1]!=1) continue

var combinationSum2 = function(candidates, target) {
    const res = []  // 结果[][]
    const path = [] // 每次递归的结果[]
    let sum = target
    const used = new Array(candidates.length)		//初始化特定长度的数组
    candidates = candidates.sort((a,b)=>a>b?1:-1)	//数组按升序排列
    console.log(candidates)
    // startIndex ：每次递归的起使位置
    const backtracking = (startIndex)=>{
        if (sum < 0) { // 剪枝操作
            return; // 如果path.size() == k 但sum != n 直接返回
        }
        if( sum===0 ){		//终止条件
            res.push([...path])		
            return
        }
        for(let i=startIndex; i< candidates.length; i++){	// 本层集合中元素
            if(sum-candidates[i] < 0 ) continue //剪枝优化
            if(i>0&&candidates[i]===candidates[i-1]&&used[i-1]!=1) continue //树层去重
            path.push(candidates[i])	
            sum-= candidates[i]	
            used[i]=1		
            backtracking(i+1)		//树枝去重
            path.pop()
            sum+= candidates[i]	
            used[i]=0		
        }
    }
    backtracking(0)
    return res
};

注意JS中：

数组按升序排列的实现
初始化特定长度的数组

组合总和II ​

思路 ​

树层去重 ​

组合总和II

思路

树层去重