组合总和III

Question

找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：

只使用数字1到9
每个数字最多使用一次

返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次，组合可以以任何顺序返回。

思路

相比于组合只需要添加判断和是否为n的逻辑即可

这里使用一个全局变量来计算减法，统计和是否为n

var combinationSum3 = function(k, n) {
    const res = []  // 结果[][]
    const path = [] // 每次递归的结果[]
    let sum = n
    // startIndex ：每次递归的起使位置
    const backtracking = (n, k, startIndex)=>{
        if(path.length===k){		
            if(sum===0)
                res.push([...path])		
            return
        }
        for(let i=startIndex;i<= 9;i++){	// 本层集合中元素
            path.push(i)	
            sum-=i			
            backtracking(n,k,i+1)		
            path.pop()
            sum+=i			
        }
    }
    backtracking(n,k,1)
    return res
};

剪枝

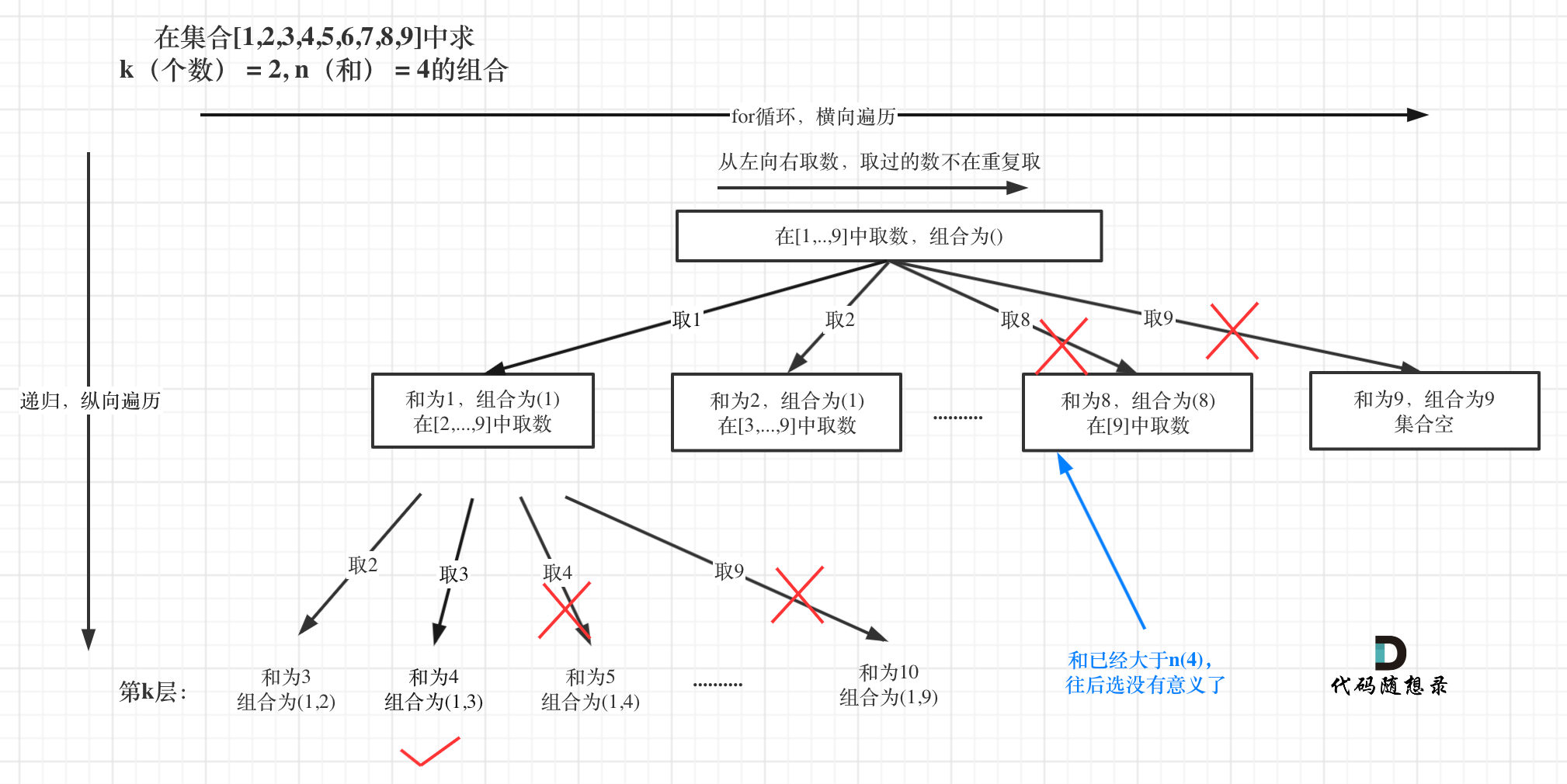
已选元素总和如果已经大于n（图中数值为4）了，那么往后遍历就没有意义了，直接剪掉。

那么剪枝的地方可以放在递归函数开始的地方，代码如下：

var combinationSum3 = function(k, n) {
    const res = []  // 结果[][]
    const path = [] // 每次递归的结果[]
    let sum = n
    // startIndex ：每次递归的起使位置
    const backtracking = (n, k, startIndex)=>{
        if (sum < 0) { // 剪枝操作
            return; // 如果path.size() == k 但sum != n 直接返回
        }
        if(path.length===k){		
            if(sum===0)
                res.push([...path])		
            return
        }
        for(let i=startIndex;i<= 9;i++){	// 本层集合中元素
            path.push(i)	
            sum-=i			
            backtracking(n,k,i+1)		
            path.pop()
            sum+=i			
        }
    }
    backtracking(n,k,1)
    return res
};

组合总和III ​

思路 ​

剪枝 ​

组合总和III

思路

剪枝