Cocolib

Appearance

On this page

打家劫舍 ​

TIP

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

思路 ​

一开始想法比较简单：

  • 偶数下标相加，奇数下标相加
  • 结果返回最大值
js
var rob = function(nums) {
    let even = 0
    let odd = 0
    for(let i=0;i<nums.length;i++){
        if(i%2===0) even += nums[i]
        else    odd += nums[i]
    }
    return Math.max(even,odd)
};

但是不能通过所有样例：

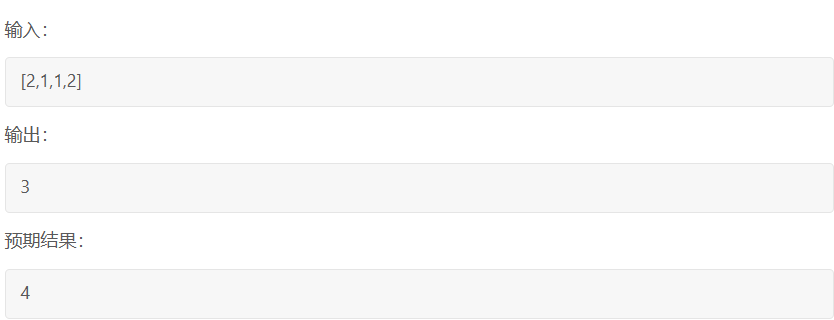
image-20230627115424131

当前房屋偷与不偷取决于 前一个房屋和前两个房屋是否被偷了

  1. 确定dp数组（dp table）以及下标的含义

dp[i]：考虑下标i（包括i）以内的房屋，最多可以偷窃的金额为dp[i]。

  1. 确定递推公式

决定dp[i]的因素就是第i房间偷还是不偷。

如果偷第i房间，那么dp[i] = dp[i - 2] + nums[i] ，即：第i-1房一定是不考虑的，找出 下标i-2（包括i-2）以内的房屋，最多可以偷窃的金额为dp[i-2] 加上第i房间偷到的钱。

如果不偷第i房间，那么dp[i] = dp[i - 1]，即考虑i-1房，（注意这里是考虑，并不是一定要偷i-1房，这是很多同学容易混淆的点）

然后dp[i]取最大值，即dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);

  1. dp数组如何初始化

从递推公式dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);可以看出，递推公式的基础就是dp[0] 和 dp[1]

从dp[i]的定义上来讲，dp[0] 一定是 nums[0]，dp[1]就是nums[0]和nums[1]的最大值即：dp[1] = max(nums[0], nums[1]);

js
var rob = function(nums) {
    let dp = []
    dp[0] = nums[0]
    dp[1] = Math.max(nums[0],nums[1])
    for(let i=2;i<nums.length;i++){
        dp[i] = Math.max(dp[i-2]+nums[i],dp[i-1])
    }
    return dp[nums.length-1]
};