Cocolib

Appearance

On this page

路径总和 ​

Question

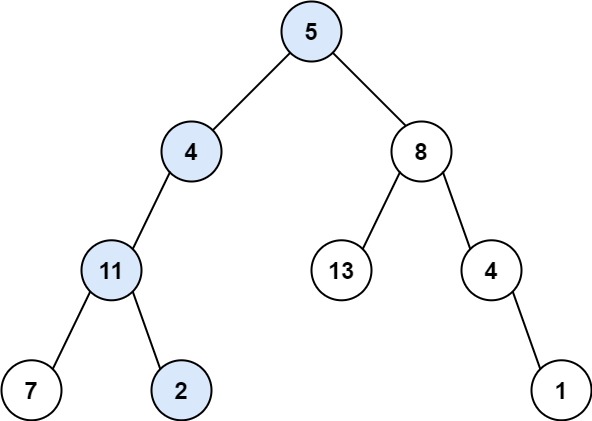
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

img

方案一 ​

先前序遍历求出所有路径，将他们的和依次和targetSum进行对比

此时的递归函数没有返回值

js
var hasPathSum = function(root, targetSum) {
    const path = [] //暂时存放路径
    const res = []
    digui(root,path,res)
    console.log(res)
    let flag = false
    res.forEach((value)=>{
        if(value===targetSum)   
            flag = true
    })
    return flag
};

var digui = function(root,path,res){     //前序遍历
    if(root===null) return
    path.push(root.val)		
    if(root.left===null&&root.right===null){    //遍历到叶子结点
        let s=0
        path.forEach((value)=> s+=value) 
        res.push(s)
        console.log(s)
    }	    
    if(root.left!=null) {
        digui(root.left,path,res) 
        path.pop()					//回溯
    }
    if(root.right!=null) {
        digui(root.right,path,res) 
        path.pop()					//回溯
    }
}

方案二 ​

有返回值的情况

以使用深度优先遍历的方式（本题前中后序都可以，无所谓，因为中节点也没有处理逻辑）来遍历二叉树

确定递归函数的参数和返回类型 ​

参数：需要二叉树的根节点，还需要一个计数器，这个计数器用来计算二叉树的一条边之和是否正好是目标和，计数器为int型。

再来看返回值，**递归函数什么时候需要返回值？什么时候不需要返回值？**这里总结如下三点：

  • 如果需要搜索整棵二叉树且不用处理递归返回值，递归函数就不要返回值。
  • 如果需要搜索整棵二叉树且需要处理递归返回值，递归函数就需要返回值。
  • 如果要搜索其中一条符合条件的路径，那么递归一定需要返回值，因为遇到符合条件的路径了就要及时返回。

而本题我们要找一条符合条件的路径，所以递归函数需要返回值，及时返回，那么返回类型是什么呢？

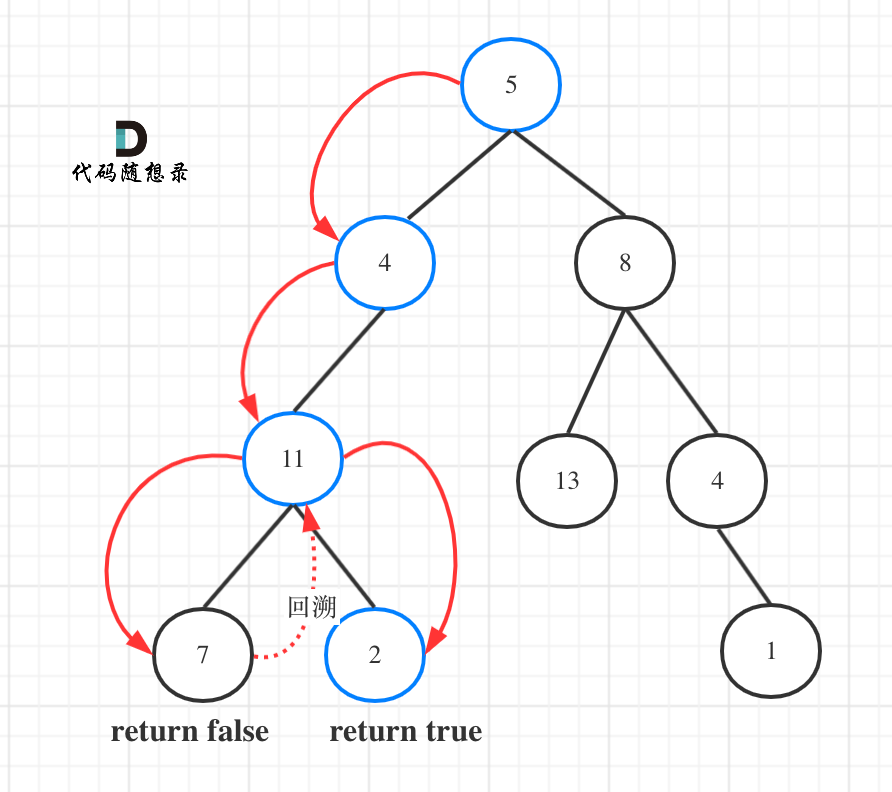
112.路径总和

图中可以看出，遍历的路线，并不要遍历整棵树，所以递归函数需要返回值，可以用bool类型表示。

确定终止条件 ​

首先计数器如何统计这一条路径的和呢？

不要去累加然后判断是否等于目标和，那么代码比较麻烦，可以用递减，让计数器count初始为目标和，然后每次减去遍历路径节点上的数值。

如果最后count == 0，同时到了叶子节点的话，说明找到了目标和。

如果遍历到了叶子节点，count不为0，就是没找到。

确定单层递归的逻辑 ​

因为终止条件是判断叶子节点，所以递归的过程中就不要让空节点进入递归了。

递归函数是有返回值的，如果递归函数返回true，说明找到了合适的路径，应该立刻返回。

js
//返回值是 boolean
var hasPathSum = function(root,targetSum){   
    if(root===null) return false  
    return digui(root,targetSum-root.val)
}
var digui = function(root,targetSum){
    if(root.left===null&&root.right===null && targetSum === 0){    //遇到叶子节点，并且计数为0
        return true
    }
    if(root.left===null&&root.right===null && targetSum != 0){    //遇到叶子节点而没有找到合适的边，直接返回
        return false
    }
    if(root.left!=null){    //遍历左子树
        if(digui(root.left,targetSum-root.left.val)) return true    //包含回溯
    }
    if(root.right!=null){    //遍历右子树
        if(digui(root.right,targetSum-root.right.val)) return true  //包含回溯
    }
    return false
}