不同的二叉搜索树
TIP
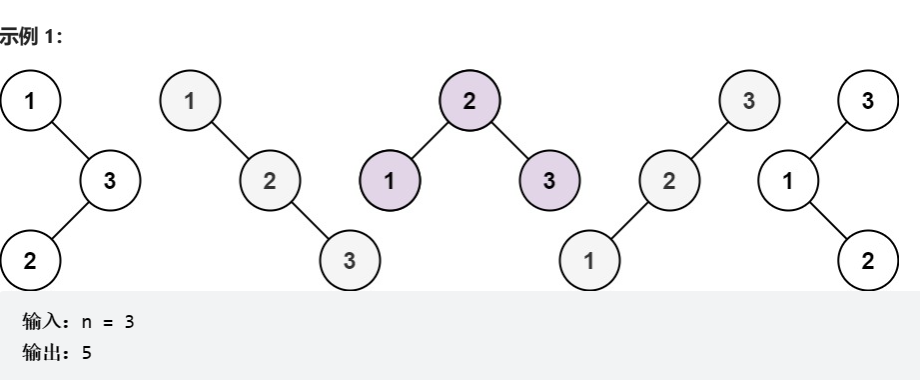
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
思路
动规五部曲
- 确定dp数组以及下标的含义:
1到i为节点组成的二叉搜索树的个数为dp[i] - 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
js
var numTrees = function(n) {
let dp = []
dp[0] = 1 //空的二叉树也是二叉搜索树
dp[1] = 1
dp[2] = 2
for(let i=3;i<=n;i++){
dp[i] = 0
for(let j=0;j<=i-1;j++){
dp[i] += dp[j]*dp[i-j-1]
}
}
return dp[n]
};最难的是确定递归公式:
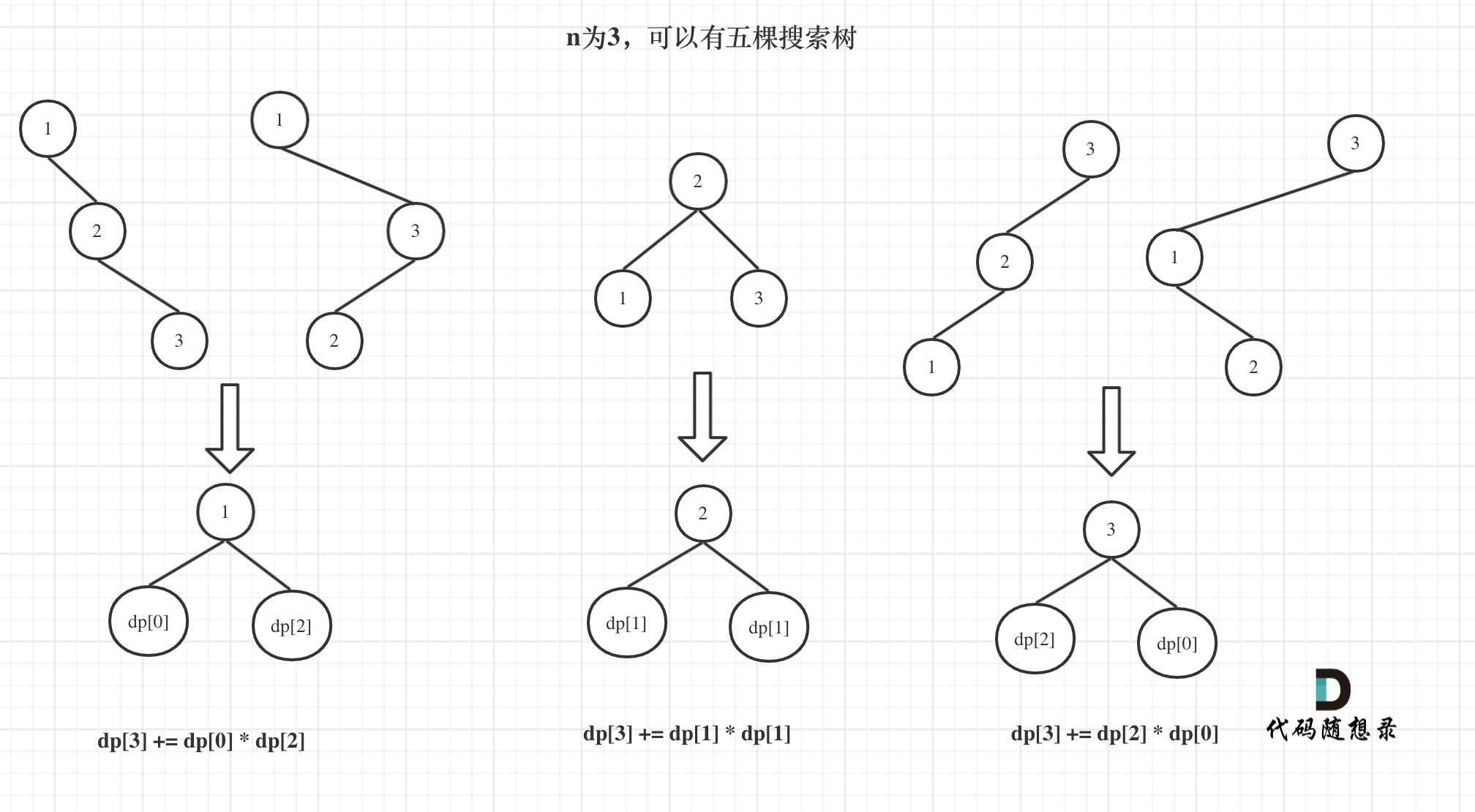
dp[3],就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量
元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量
元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量
元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量
有2个元素的搜索树数量就是dp[2]。
有1个元素的搜索树数量就是dp[1]。
有0个元素的搜索树数量就是dp[0]。
所以dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]
 Cocolib
Cocolib